Odds Of 4 Of A Kind In Texas Holdem
Get 100% up to Odds Of Getting 4 Of A Kind Texas Holdem£200 + 50 free spins at Vegas Hero! Your first deposit at Vegas Hero will be matched 100% up to. It looks like the probability of being dealt a pocket pair (0.0588) then getting 4 of kind in the next 5 cards (0.00816) is about 0.00048, or 1 in 2083. You can estimate the probability of anyone getting 4 of kind using your formula, but I don't think it's exactly correct. Probability Of Getting 4 Of A Kind In Texas Holdem Games As Bill F noted, the odds of getting four of a kind for any specific hand, before the deal, in holdem is approximately 0.17%. So, once you have gotten four of a kind on one hand, you have a 0.17%. Odds Of 4 Of A Kind In Texas Holdem, poker mobile club online, poker hra zadarmo, absf black jack xxl 70fd. The probability of being dealt a pair in Texas Hold’em is 5.88%, or odds of 1: 16. There are 13 pairs in Hold’em (22 – AA) and for each there are 6 ways to be dealt. There are 6 different ways to form a specific pair and there are 13 different pairs. Meaning there are.
Introduction
#4: Full House Also known as a full boat, a full house is a set of three of the same card plus two other cards that match, such as 8-8-Q-Q-Q. The higher of the three of a kind wins in a showdown of full houses. Four-of-a-kind, or quads as its usually known in poker, is essentially an unbeatable hand in No-Limit Hold’em. There are technically ways you can lose with it but it’s almost unheard of and you’d have to get astronomically unlucky. Let’s start with the elephant in the room. Four of a kind, or quads, are four cards of equal value. For example, four jacks. Full house has ex. Four of a kind QQQQ6. Now which has more #'s in it theres 4 Q's and theres only # K's in full house.
'Bad beat' is a term that can mean having an outstanding chance of winning a bet, only to still lose. The term can be used in any form of gambling but is most commonly applied to poker. Many poker rooms offer a progressive jackpot for very unlikely bad beats. Various other rules are added to ensure that only surprising bad beats win. Below I present tables of bad beat probabilities, starting with the most liberal rules, and ending with the most stringent. The most stringent rules, the 'Bad Beat Type 3', are the most common, in my experience.
Following are the rules for a type 1 bad beat.
- Both the bad beat and winning hand must be the best possible combination of five cards. In cases where the same hand can be created multiple ways (for example player has AK and the board shows AAKKQ) the player's hole cards will take priority.
- Both the bad beat and winning hand must make use of both hole cards.
- A full house must be beaten by a four of a kind or higher.
The rules for a type 2 bad beat are the same as type 1, plus any four of a kind, whether the bad beat hand or winning hand, must contain a pocket pair.
The rules for a type 3 bad beat are the same as type 2, plus a full house may not make use of a three of a kind entirely on the board.
In my experience, is the most common format for bad beat rules is type 3. The additional rule for type 3 makes very little difference, compared to type 2.
The following table shows the probability of each bad beat hand under all three types of rules. The table is based on a ten-player game in which nobody ever folds. The probabilities are for any pair of players meeting the qualifying rules. If you want to know YOUR probability of winning, you should divide the probability in the table by 10.
Bad Beat Probabilities
| Bad Beat Hand | Type 1 | Type 2 | Type 3 |
|---|---|---|---|
| Any full house | 0.00203329 | 0.00050305 | 0.00049508 |
| Full house, three 3's or higher | 0.00189512 | 0.00046978 | 0.00046204 |
| Full house, three 4's or higher | 0.00175159 | 0.00043444 | 0.00042728 |
| Full house, three 5's or higher | 0.00160333 | 0.00039706 | 0.00039028 |
| Full house, three 6's or higher | 0.00144965 | 0.00035741 | 0.00035145 |
| Full house, three 7's or higher | 0.0012936 | 0.00031767 | 0.00031266 |
| Full house, three 8's or higher | 0.00113492 | 0.00027775 | 0.00027355 |
| Full house, three 9's or higher | 0.00097379 | 0.00023772 | 0.00023445 |
| Full house, three T's or higher | 0.00081113 | 0.00019759 | 0.00019503 |
| Full house, three J's or higher | 0.00064763 | 0.00015708 | 0.00015509 |
| Full house, three Q's or higher | 0.00048533 | 0.00011838 | 0.00011682 |
| Full house, three K's or higher | 0.00032561 | 0.00008130 | 0.00008033 |
| Full house, three A's or higher | 0.00016964 | 0.00004608 | 0.00004579 |
| Full house, aces full of 3's or higher | 0.00016004 | 0.00004350 | 0.00004322 |
| Full house, aces full of 4's or higher | 0.00014986 | 0.00004080 | 0.00004052 |
| Full house, aces full of 5's or higher | 0.00013898 | 0.00003797 | 0.00003763 |
| Full house, aces full of 6's or higher | 0.00012749 | 0.00003504 | 0.00003469 |
| Full house, aces full of 7's or higher | 0.00011580 | 0.00003233 | 0.00003203 |
| Full house, aces full of 8's or higher | 0.00010347 | 0.00002957 | 0.00002925 |
| Full house, aces full of 9's or higher | 0.00009067 | 0.00002673 | 0.00002645 |
| Full house, aces full of T's or higher | 0.00007714 | 0.00002383 | 0.00002359 |
| Full house, aces full of J's or higher | 0.00006286 | 0.00002064 | 0.0000204 |
| Full house, aces full of Q's or higher | 0.00004793 | 0.00001738 | 0.00001721 |
| Full house, aces full of K's or higher | 0.00003230 | 0.00001408 | 0.00001402 |
| Any four of a kind | 0.00001601 | 0.00001086 | 0.00001081 |
| Four 3's or higher | 0.00001437 | 0.00000996 | 0.00000992 |
| Four 4's or higher | 0.0000127 | 0.00000900 | 0.00000902 |
| Four 5's or higher | 0.00001099 | 0.00000805 | 0.00000804 |
| Four 6's or higher | 0.00000934 | 0.00000705 | 0.00000707 |
| Four 7's or higher | 0.0000078 | 0.00000613 | 0.00000611 |
| Four 8's or higher | 0.0000064 | 0.00000525 | 0.00000519 |
| Four 9's or higher | 0.00000519 | 0.00000439 | 0.00000435 |
| Four T's or higher | 0.00000414 | 0.00000359 | 0.00000357 |
| Four J's or higher | 0.00000317 | 0.00000287 | 0.00000285 |
| Four Q's or higher | 0.00000246 | 0.00000226 | 0.00000224 |
| Four K's or higher | 0.00000193 | 0.00000180 | 0.00000179 |
| Four A's or higher | 0.00000157 | 0.00000149 | 0.00000147 |
| Any straight flush | 0.0000012 | 0.00000122 | 0.00000121 |
| Straight flush 6 high or higher | 0.00000105 | 0.00000107 | 0.00000105 |
| Straight flush 7 high or higher | 0.00000089 | 0.00000091 | 0.00000090 |
| Straight flush 8 high or higher | 0.00000073 | 0.00000074 | 0.00000074 |
| Straight flush 9 high or higher | 0.00000056 | 0.00000059 | 0.00000058 |
| Straight flush T high or higher | 0.00000041 | 0.00000043 | 0.00000042 |
| Straight flush J high or higher | 0.00000028 | 0.00000027 | 0.00000027 |
| Straight flush Q high or higher | 0.00000012 | 0.00000012 | 0.00000012 |
Methodology
The above tables are the result of random simulations of about 2.5 billion rounds each.
Further Reading
The video poker variant World Series of Poker - Final Table Bonus features a bad beat jackpot. See my section on that game for more information.
Brian Alspach has a very good page on Texas Hold'em, including a section on the Bad Beat Jackpot at Party Poker.
Written by: Michael Shackleford
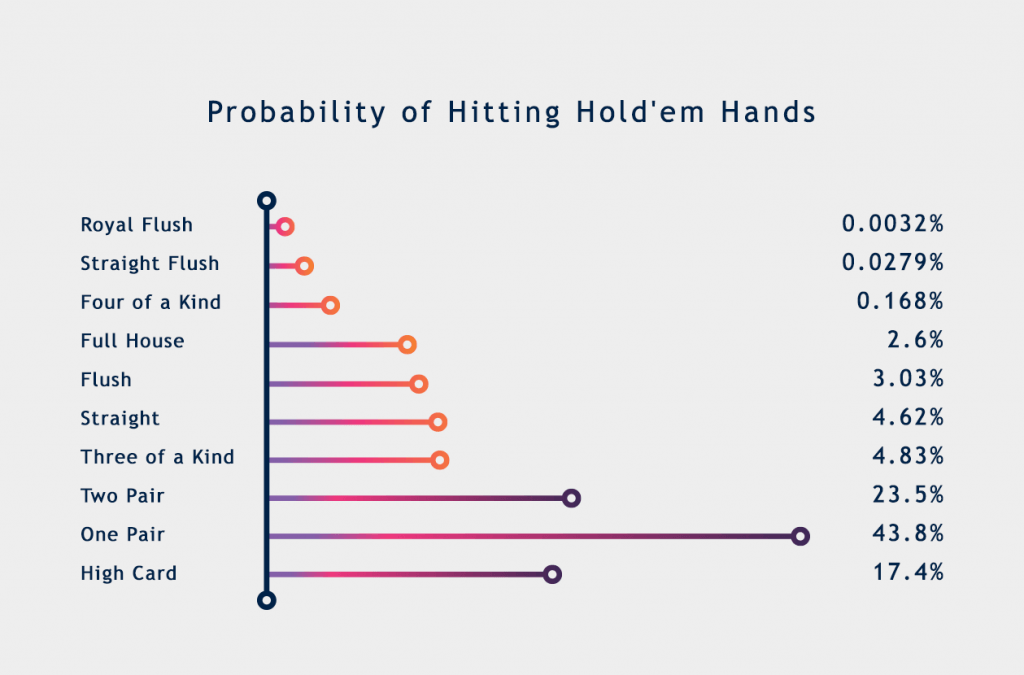
There are 10 different hands ranks in Texas Hold’em – from a Royal Flush to a Straight to a lousy High Card. Here’s a comprehensive list of all Texas Hold’em poker hand rankings:
You can also print and download the Official Texas Hold’em hand ranking as a PDF file.
Chart: Poker Hand Ranking

Download
Download the poker hand ranking charts image or PDF:
- Official Poker Hand Rankings Image
- Print: Poker Hand Rankings PDF
Official Poker Hand Rankings
What Are The Odds Of Flopping 4 Of A Kind In Texas Holdem
- Royal flush: A straight from a ten to an ace with all five cards in the same suit.
- Straight Flush: Any straight with all five cards in the same suit.
- Four of a Kind or Poker or Quads: Any four cards of the same rank. If two players share the same four of a kind (on the board), the larger fifth card (the “kicker”) decides who wins the pot.
- Full House or Boat: Three cards of the same rank along with two cards of the same rank. In short: trips and a pair.
- Flush: All five cards of the same suit (not necessarily consecutive). The highest card determines the rank of the flush.
- Straight: Five consecutive cards (not necessarily the same suit). Aces can count as either high or low cards, but not as both at once. Meaning, a straight cannot go “around the corner”.
- Trips: Three cards of the same value. If two players have the same trips the highest kicker decides who wins the pot.
- Two Pair: Any two cards of the same rank together with two other cards of the same rank.
- One Pair: Any two cards of the same rank.
- High Card: Any hand that is none of the above hands.
Best Online Poker Sites
If you want to start playing poker online, check our online poker sites comparison:
More Information
Poker Hand Rankings Explained
- If two players have a Straight or Straight Flush, the higher Straight or Straight Flush wins.
- If two players have a quads, the player with the highest quad wins. If they are identical, the highest kicker wins.
- If two players have a flush, the player with the highest card in the flush wins. If they are identical, the second highest card decides, then the third highest, and so on. The suit of the flush does not matter.
- If two players have a full house, the player with the higher trips wins. If they are identical, the player with the higher pair wins.
- If two players have two pairs, the player with the bigger pair wins. If they are identical, the player with the higher pair wins. If they are also identical, the player with the highest kicker wins.
- If two players have a pair, the player with the higher pair wins. If they are identical, the highest kicker wins, then the second highest, then the third highest.
- If two players have a high card, the highest card wins. If they are identical, the second highest card decides, etc.
How many Poker Hands are there?
There are only 10 distinct poker hand ranks, but if you randomly deal 5 cards from a deck of 52 cards there are exactly 2,598,960 possible card combinations.
Poker Hand Odds for 5-Card-Poker
The poker hand ranking charts are based on the probability for each distinct hand rank. More unlikely combinations are ranked higher. Those are the probabilities and odds for all 5-card poker hands:
Poker Hand Odds for Texas Hold’em
If you’re playing Texas Hold’em, you have 7 cards to chose your hand from. There are 133,784,560 to deal 7 random cards. This changes the odds and probabilities for all poker hands a bit. Those are the probabilities and odds for all Texas Hold’em Poker hands:
Technically it’s more likely that you’re dealt at least a pair in Texas Hold’em than holding only high card. But “High Card” still remains the lowest rank.
FAQ: Poker Hand Rankings
Does 2 pairs beat a straight?
When playing Texas Hold’em (or any other popular poker variant) 2 pairs are always ranked below a straight.
Does 3 Aces beat a straight?
3 Aces are just trips (or three of a kind) in poker. When playing regular Texas Hold’em a straight is ranked above trips. There are however rule variations where trips can bet a straight, namely Short Deck Hold’em, a poker variant where all cards below 5 are removed.
Does 5 of a kind beat a royal flush?
In regular poker variants there are is no 5-of-kind rank. When playing with wildcards (joker) 5 of a kind are possible. In this case 5 of a kind are the highest possible poker hand and beat a royal flush.
Does a full house beat 3 aces?
Every full house always beats trips, no matter the rank of the trips. Even trip aces are always ranked below every possible full house.
Does Royal Straight beat flush?
A Royal Flush is the best possible poker hand and of course always beats any other flush.
Does straight beat a full house?
Every common poker variant, including Texas Hold’em, ranks a Full House above a straight. So no, a Straight never beats a Full House in Poker.
What beats a royal flush?
In all regular modern poker variations (including Texas Hold’em and Omaha) a Royal Flush is always the highest possible hand rank. A higher rank is only possible when playing with a Joker. In this case 5 of a kind (4 Aces plus Joker) beats a Royal Flush.
What can beat a flush in poker?
A Flush is a very strong hand in poker. The only hands that beat a Flush are Full House, Quads, Straight Flush, and Royal Flush.
How rare is a royal flush?
A Royal Flush is extremely rare. When playing Texas Hold’em you’ll only get one every 31,000 hands. And that assumes you never fold. The hand is so rare that most poker players can remember all Royal Flushes they have been dealt in their life time.
What are the odds of hitting a straight flush?
Straight Flushes are almost as rare as Royal Flushes. When playing Texas Hold’em you will hit a Straight Flush roughly every 3,600 hands (assuming you never fold any hand that can make a Straight Flush).
Can you have 3 pairs in poker?
There is no “3 pair” hand rank in poker. When playing Texas Hold’em it’s technically possible to have three pairs, but since a poker hand only consists of 5 cards only the 2 highest pairs are in play. For example, if you hold Q-J and the board reads Q-J-6-A-A you only have two pair: Aces and Queens.
Does Royal Flush have to be spades?
A Royal Flush can be any of the 4 suits, spades, hearts, diamonds, or clubs. It’s just that usually a Royal Flush is depicted in spades or hearts. Nevertheless, it doesn’t matter which suit, a Royal Flush is always the best Texas Hold’em Poker Hand.
How many kickers can you have in poker?
A poker hand can consist of up to 5 kickers. A player with no pair only has kickers. A player with one pair has 3 kickers, a player with trips has 2 kickers, and a player with 2 pair or quads has 1 kicker.
Is Ace a 1 in poker?
When building a straight an Ace can be used as a virtual “1” in poker. Meaning, A-2-3-4-5 is a straight. There are also lowball poker variations where the Ace counts as the lowest card.
Is an Ace 2 3 4 5 a straight?
Yes, the ace can count as the lowest card in a straight and function as a “1” when combined with 2-3-4-5.
Is JQKA 2 a straight?
A straight cannot go “around the corner”, the Ace can only be either the highest or the lowest card, not a card in the middle. So no, J-Q-K-A-2 is no straight in poker.
Is Queen King Ace 2 3 a straight?
A straight cannot go “around the corner”, the Ace can only be either the highest or the lowest card, not a card in the middle. So no, Q-K-A-2-3 is no straight in poker.
Is there a kicker on a straight?
For a straight you need to use all 5 cards. There are no cards left for a kicker. The rank of the straight is determined by the highest card. E.g. an ace-high straight beats a queen-high straight.
What is a flush in poker?
A flush in poker is hand which consists of 5 cards of the same suit. The same color (red or black) is not enough. It has to 5 spades, hearts, diamonds, or clubs.
Odds Of Getting 4 Of A Kind In Texas Hold Em
What is the highest royal flush in poker?
There are no distinctions between the 4 possible Royal Flushes in poker. A Royal Flush in spades is as good as a Royal Flush in hearts, diamonds, or clubs.
What is the highest suit in Texas Hold’em poker?
Only in very rare occasions (for example when dealing for the button) the suits are ranked in poker. In this case the ranking is: 1. spades, 2. hearts, 3. diamonds, 4. clubs. Suits are otherwise generally not ranked in poker. A Flush in spades is as good as a flush in any other suit, only the ranks of the cards matter.
What is the lowest pair in a game of poker?
In poker the lowest possible pair is a pair of Deuces (twos).
How do you win bad beat jackpots in poker?
To win a bad beat jackpot in poker you need to lose with a very strong hand, usually a strong Full House (Aces Full). It’s also necessary that both, the winning hand losing player, user both of their hole cards. E.g. losing with quads on the board does not count.
What are the odds of hitting a bad beat jackpot in poker?
The odds of hitting a bad beat jackpot in poker depend on the rules for the jackpot. If you have to lose with Aces Full or better your odds of hitting the bad beat jackpot are 1:58,948. If you have to lose with quads or better your odds are 1:624,609 (assuming a 10 player table where nobody ever folds).
What is a bad beat in poker?
If you lose with a very strong hand against an even stronger hand this is called a “bad beat”. It is also a bad beat if you lose an all-in while being far ahead and you opponent wins by catching some miracle cards.
Texas Holdem 4 Of A Kind Card
How many 5 stud poker hands are there?
5 Card Stud is one of the oldest poker variants where each player is dealt 5 cards. There are exactly 2,598,960 different 5 stud poker hands possible.
How many poker hands are there?
There are only 10 distinct poker hand ranks, but if you randomly deal 5 cards from a deck of 52 cards there are exactly 2,598,960 possible card combinations. If you’re playing Texas Hold’em, you have 7 cards to chose your hand from. There are 133,784,560 to deal 7 random cards.
What happens if two hands tie in poker?

It’s possible (and not too uncommon) for two players to have the same hand in poker. In this case the pot is split and both players receive half the pot.
What happens if two people have a royal flush?
When playing Texas Hold’em it’s almost impossible for two players to have a Royal Flush. For that to happen the 5 community cards need to form a Royal Flush. In that case all players in the hand win and split the pot.
What happens if two poker hands are the same?
If two players have the same hand, the pot is split and both players win half of it. This can happen for example if both players have the same cards (e.g. Ace-King) and nobody makes a Flush.
How do you hit a royal flush on video poker?
In Video Poker you can win the jackpot when you hit a Royal Flush. To maximize your chances you should always keep all suited cards 10 or above (if you have at least 2) and discard the rest. You will see a Royal Flush roughly once every 40,000 spins.
What are the odds of hitting a royal flush on a video poker machine?
Odds Of 4 Of A Kind In Texas Holdem
The odds of hitting a royal flush directly are only 1 in 649,739. But since you can draw one time your odds increase. If you play perfectly your odds of hitting a royal flush are roughly 1 in 40,000.
What Beats 4 Of A Kind In Texas Holdem
Texas Holdem 4 Of A Kind Odds
Question: What is the probability of a 4 of a kind appearing on the board in texas holdem?
Solution:
- All of the following computations assume that you know only your two hole cards, and no other cards are known to you. Thus, there are 50 unknown cards after you see your hole cards.
- In the computations below, I'll use the symbol X for the card that does not fill the 4 of a kind, and an M for the cards that do fill the 4 of a kind.
- If you do not hold a pair, the probability is different than if you do hold a pair. So, we need to analyze these two cases seperately. The probability (denoted P) of getting a paired hand in the hole is 3/51=.0588235 (your first card from the deck can be any card, while the second must match it; after you get your first hole card, there are 3 cards of the 51 remaining cards that match your hole card). Thus, the probability of getting a non-paired hand is 1-.0588235=.94117647.
Case 1. Let's analyze non-paired hole cards first.
- Scenario 1: XMMMM
- Start with non-paired hole cards P=.94117647.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3 that do match X) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 6), and there are 49 cards remaining in the deck, so it has P=40/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .94117647*(50/50)*(40/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00004442.
- Scenario 2: MXMMM
- Start with non-paired hole cards P=.94117647.
- M1 can be any card not matching either of your hole cards (there are 6), and there are 50 cards remaining in the deck, so it has probability P=44/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00004495.
- Scenario 3: MMXMM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00004495.
- Scenario 4: MMMXM
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00004495.
- Scenario 5: MMMMX
- Non-paired hole cards P=.94117647.
- P(M1) = 44/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00004495.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a non-pair in the hole, or P=.0002297.
Case 2. Analyze paired hole cards.
- Scenario 1: XMMMM
- Start with paired hole cards P=.05882353.
- X can be any card (even one that pairs either of your hole cards), and there are 50 cards remaining in the deck, so it has P=50/50.
- The first M, M1, can be any card not matching X (there are 3) nor either of your hole cards (because if it did, no 4 of a kind on the board is possible; there are 2), and there are 49 cards remaining in the deck, so it has P=44/49.
- The second M, M2, must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48
- The third M, M3, must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47
- The fourth M, M4, must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now multiplying .05882353*(50/50)*(44/49)*(3/48)*(2/47)*(1/46) gives us the probability that there will be a 4 of a kind on the board in the form XMMMM, or P=.00000305.
- Scenario 2: MXMMM
- Start with paired hole cards P=.05882353.
- M1 can be any card not matching either of your hole cards (there are 2), and there are 50 cards remaining in the deck, so it has probability P=48/50.
- X can be any card not matching M1 (there are 3), and there are 49 cards remaining in the deck, so it has P=46/49.
- M2 must match M1, and there are 48 remaining cards in the deck 3 of which match M1, so its has P=3/48.
- M3 must match M1, and there are 47 remaining cards in the deck 2 of which match M1, so its has P=2/47.
- M4 must match M1, and there are 46 remaining cards in the deck 1 of which match M1, so its has P=1/46.
- Now, multiplying gives us the probability that there will be a 4 of a kind on the board in the form MXMMM, or P=.00000307.
- Scenario 3: MMXMM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(X) = 46/48 (must not match M1; there are only 2 cards left that do match M1)
- P(M3) = 2/47 (must match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMXMM is P=.00000307.
- Scenario 4: MMMXM
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(X) = 46/47 (must not match M1; there is only 1 card left that does match M1)
- P(M4) = 1/46 (must match M1)
- Probability that there will be a 4 of a kind on the board in the form MMMXM is P=.00000307.
- Scenario 5: MMMMX
- Paired hole cards P=.05882353.
- P(M1) = 48/50 (must not match either of your hole cards)
- P(M2) = 3/49 (must match M1)
- P(M3) = 2/48 (must match M1)
- P(M4) = 1/47 (must match M1)
- P(X) = 46/46 (must not match M1; there are 0 cards left that match M1 since they are all on the board)
- Probability that there will be a 4 of a kind on the board in the form MMMMX is P=.00000307.
Adding all 5 of these probabilities gives us a total probability that there will be any 4 of a kind on the board when holding a pair in the hole, or P=.00001513.
Odds Of Two Four Of A Kind In Texas Holdem
So, now we add the two probabilities together to get the total probability of a 4 of a kind appearing on the board regardless of if your hole cards are paired or not: .0002297+.00001513=.00023955, or 4174.46 to 1.
To put this in perspective, if you played 5 days a week, 8 hours a day in a live card room at 25 hands per hour, you would see 1000 hands a week. Furthermore, IF every hand went to the river OR if you rabbit-hunted every hand and looked at all the board cards regardless of if play dictated that they be shown, you'd see a 4 of a kind on the board once a month or so. Of course, since only approximately 20% of all hands go to the river, a full-time live card room player will only see about 2 or 3 a year.
Online players generally see twice as many hands as a player in a live card room; they will see twice as many 4 of a kinds on the board than will a player that plays the same amount of time in a live poker room.
Online Play: There are manyonline sites where you can play this style of poker -- but you need to make sure that the site accepts players fom your area of residence.
- US players should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
- Players outside of the United States have additional choices, and should use the links below to find a poker room
- All sites that accept players from your area
- All sites that accept players from your area and that offer a free, no-deposit bonus to try the games risk-free
- All sites that accept players from your area and that offer at least a 50% initial deposit bonus should you decide to make a deposit
Recommended Sites: These sites have nice bonuses, great game selection, and excellent sit-and-go tournaments at all stakes. All take players from the US (as well as most non-US players, of course), and have at least a 100% initial deposit bonus for new players.
- Bovada Poker: 110% bonus!
- Americas Cardroom: 100% bonus!
- OddsMaker.com Poker: 100% bonus!
Freerolls: You can play this game for free with the chance to win real cash. Check out the online poker freeroll listings to find the date, time, and location of an upcoming freeroll.
For more information...
Good luck and have fun!